Hogyan számítsuk ki az egyenlő szárú háromszög magasságát?
Emlékszünk még a középiskolai matekórákra? Akkoriban talán nem is sejtettük, hogy az olyan egyszerűnek tűnő fogalmak, mint a háromszög vagy a magasság, mennyi érdekességet és hasznos tudást rejtenek. Ma egy ilyen témát járunk körbe közösen: az egyenlő szárú háromszög magasságának kiszámítását.
Nem kell matekzseninek lennünk hozzá, csak egy kis odafigyelésre és néhány egyszerű képletre lesz szükségünk.
Mi is az az egyenlő szárú háromszög?
Kezdjük az alapoknál. Egy egyenlő szárú háromszög olyan háromszög, amelynek két oldala egyenlő hosszú. Ezt a két oldalt szárnak hívjuk, míg a harmadik, eltérő hosszúságú oldalt alapnak nevezzük.
Ezeket a tulajdonságokat érdemes megjegyezni:
- Két szára azonos hosszúságú
- Az alap két végéből induló szögek egyenlők
- A magasság az alappal merőlegesen áll, és kettévágja azt
Mi az a magasság egy háromszögben?
A háromszög magassága az a szakasz, amely:
- Az egyik csúcsból indul
- Merőlegesen érkezik a szemközti oldalra (vagy annak meghosszabbítására)
Az egyenlő szárú háromszögnél, ha az egyik szárakkal bezárt csúcsból húzzuk a magasságot az alapra, akkor az a magasság egyben szögfelező és szimmetriatengely is.
Milyen adatokra van szükségünk a magasság kiszámításához?
Attól függ, mit tudunk a háromszögről. Ezekből indulhatunk ki:
- Tudjuk a szár hosszát és az alap hosszát
- Tudjuk az oldalak hosszát és a bezárt szöget
- Tudjuk a területet és az alap hosszát
Most pedig nézzünk végig több lehetőséget a magasság kiszámítására.

1. módszer: Pitagorasz-tétellel
Ez a legegyszerűbb eset, ha tudjuk a szár hosszát (a) és az alap hosszát (b).
Mivel az egyenlő szárú háromszög tengelyesen szimmetrikus, a magasság kettévágja az alapot.
Ezért az alap fele (b / 2) és a magasság derékszögű háromszöget alkot a szár oldalával.
A Pitagorasz-tétel szerint:
![]()
Innen kifejezve a magasságot (m):
![]()
Példa:
Tegyük fel, hogy a szár hossza 10 cm, az alap hossza pedig 12 cm.
![]()
A magasság 8 cm.
2. módszer: Terület képletével
Ha tudjuk a háromszög területét (T) és az alap hosszát (b), akkor a magasságot könnyen kiszámíthatjuk az ismert területképlettel:
![]()
Innen kifejezve a magasságot:
![]()
Példa:
Ha a háromszög területe 30 cm², és az alap hossza 6 cm, akkor:
![]()
A magasság 10 cm.
3. módszer: Szög ismeretében (szinusztétel)
Van egy másik képlet is, ha ismerjük az alap és a két szár által bezárt szöget (α).
Ekkor:
![]()
Ez akkor jön jól, ha például van egy háromszögünk, ahol:
- A szár hossza: 7 cm
- A szárak által bezárt szög (csúcsszög): 60°
Ekkor a magasság:
![]()
A magasság 3,5 cm.
Mikor melyiket használjuk?
Attól függ, milyen adat áll rendelkezésre. Összefoglalva:
| Mit tudunk? | Milyen képletet használjunk? |
|---|---|
| Szár és alap hossza | Pitagorasz-tétel |
| Terület és alap hossza | Terület képlete |
| Szár hossza és csúcsszög | Szinuszos képlet |

Gyakorlati életben mire jó ez az egész?
Jogosan merül fel a kérdés: „Na de mikor kellene nekünk ezt kiszámítani a valóságban?”
Meglepően sok helyzetben! Például:
1. Lakásfelújítás vagy barkácsolás közben
Ha egy dekorációt, polcot vagy ágyvéget szeretnénk háromszög formában, jó tudni, mekkora lesz a magassága.
2. Tetőszerkezet tervezésnél
Az egyenlő szárú háromszög gyakran jelenik meg a háztetők formájában. Ha kiszámítjuk a magasságot, tudjuk, mennyire lesz magas a tetőgerinc.
3. Kertészkedésnél vagy kerti építkezésnél
Sátrak, kerti tárolók, lugasok építésekor gyakran használunk ilyen háromszögeket.
Mire figyeljünk oda a számításoknál?
- Ha számológépet használunk, állítsuk be a szögmérés fok vagy radián módját, attól függően, milyen egységben adjuk meg a szöget.
- Ha tört számokat kapunk, érdemes kerekíteni a végeredményt (pl. két tizedesjegyre).
- Ne felejtsük el ellenőrizni, hogy a szár hosszának négyzete nagyobb legyen, mint az alap fele négyzetének értéke – különben a Pitagorasz-képlet nem ad értelmes eredményt.
Gyakorlati példa lépésről lépésre: Kerti ágyás díszítőelemének megtervezése
Tegyük fel, hogy szeretnénk a kertünkbe készíteni egy háromszög alakú fa dísztáblát egy magaságyás végébe. A forma legyen egyenlő szárú háromszög, és már tudjuk, hogy:
- Az alap legyen 100 cm
- A szárak hossza legyen 80 cm
A cél: kiszámolni a magasságot, hogy tudjuk, milyen magas lesz a díszítőelem közepe.
1. lépés: Mi van meg?
- Alap (b): 100 cm
- Szár (a): 80 cm
2. lépés: Használjuk a Pitagorasz-tételt
![]()
![]()
m≈62.45 cm
Tehát a háromszög középmagassága kb. 62,5 cm lesz.
3. lépés: Mit kezdünk ezzel?
Ez alapján már könnyedén:
- Kiszabhatjuk a fából a pontos méreteket
- Beállíthatjuk a szögeket a vágásnál
- Előre megtervezhetjük a táblán a felirat vagy a minta helyét
Miért hasznos ez?
Mert értelmet ad a mateknak. Nemcsak számolunk valamit a levegőbe, hanem valódi tárgyakat tervezünk meg.
És ez bármilyen hobbi barkácsolásnál, belsőépítészetnél, vagy kerttervezésnél előjöhet.

Összességében
Egyenlő szárú háromszög magassága egyszerűen
Ahogy láttuk, többféleképpen is kiszámolhatjuk a magasságot, attól függően, mit tudunk az adott háromszögről.
A legfontosabb képletek:
- Pitagorasz-tétel:
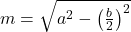
- Terület alapján:
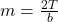
- Szinusszal:
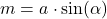
Mindegyik módszer hasznos lehet. A lényeg, hogy gondoljuk át, mit tudunk, és válasszuk a legkézenfekvőbb utat.
Lehet, hogy első ránézésre bonyolultnak tűnik a háromszög magassága, de ha lépésről lépésre haladunk, és használjuk az egyszerű képleteket, minden értelmet nyer.
És ki tudja? Lehet, hogy legközelebb, amikor saját kezűleg készítünk valamit, még jól is jön ez a tudás.
A Wiképidiáról kicsi érdekesség még…
Köszönöm a figyelmet!
Ha tetszett a cikk, ne felejtsd el megosztani barátaiddal vagy hozzászólásban megírni a véleményedet.
És ha szeretnél még hasonló tanácsokat olvasni, akkor iratkozz fel a hírlevelünkre és Likeolj minket a Facebookon!

Be the first to comment on "Így számítsuk ki az egyenlő szárú háromszög magasságát – Egyszerű képletek, érthető példák!"