A kerület számoláshoz a képletet kicsit lejjebb találod!
Kis érdekesség az elején a Wikipédiáról a kerület témakörben:
„A geometriában kerület alatt a kétdimenziós alakzatokat határoló vonal hosszát értjük. Jelentheti magát a határoló vonalat is, például a „kerület mentén” kifejezésben. A kerületet magyarul K-val rövidítjük…„
A valóságban a kerület számítás:
Az előző cikkben írtam a négyzetméter számításról, habár az egésznek a megértéséhez inkább a területszámítással kellett volna kezdeni. Mégis azért kezdtem négyzetméter számítással amivel a valós életben többször találkozhatunk vele. Most viszont jelen cikkben a kerület számításról lesz szó.
Kerület számítás egy olyan számítási módszer ami a való életben többször előfordulhat mint az iskolában megtanult másodfokú egyenletek megoldása. Itt is előfordul, hogy nem mindenki van tisztában teljes mértékben, hogy ezt a műveletet hogyan kell végezni.
Ezért teljesen az alapoktól nézzük át, az elmélettől ,a gyakorlatban előforduló megoldandó problémákig.
A kerület számítás lényege!
Mielőtt nagyon belemerülnénk a témában a kerület ( K ) számítás két alap értékből tevődik össze, van egy szélességünk, illetve van egy hosszúságnak. Ebből a két értékből, illetve ennek a két értéknek az összegéből jön ki a kerület.
Ugye itt is mint minden más számításnál alapkövetelmény hogy az a két érték azonos mértékegységben legyen megadva. Mivel legtöbbször folyómétert kell számolni ezért már a művelet megkezdése előtt érdemes mindig átváltani méterbe, így tudjuk meghatározni a folyómétert.
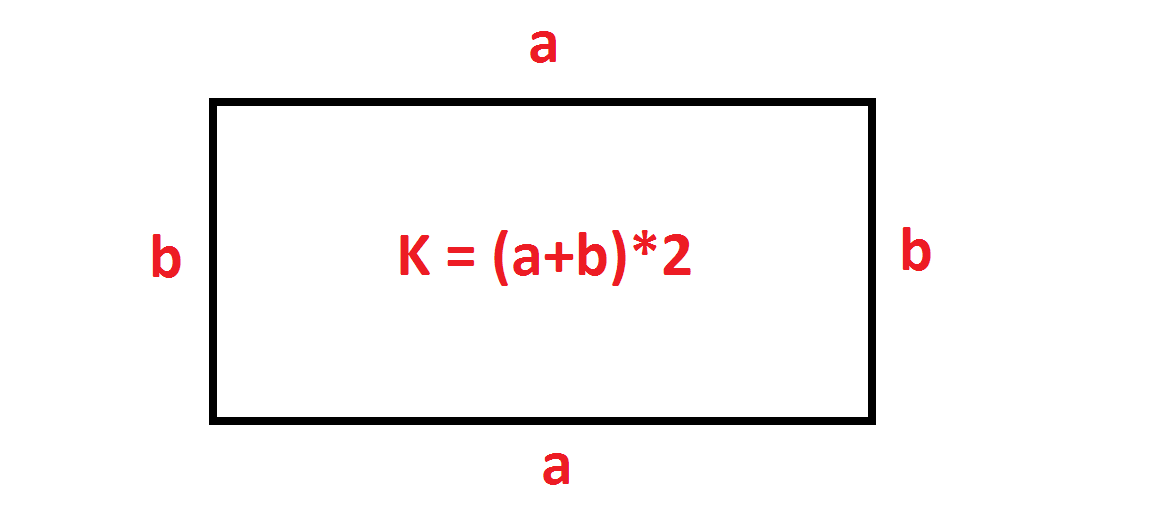
A számítás módja nagyon egyszerű. A két értéket össze kell adni egymással, majd megszorozni kettővel, így kapjuk meg a kerületet.
Következőképpen megnézzük, hogy hogyan kell alkalmazni ezt a módszert a való életben. Kerülete lehet több fajta geometriai forma is.
Egyébként a legtöbb számítási, mérési lépés azonos az összes alakzatnál:
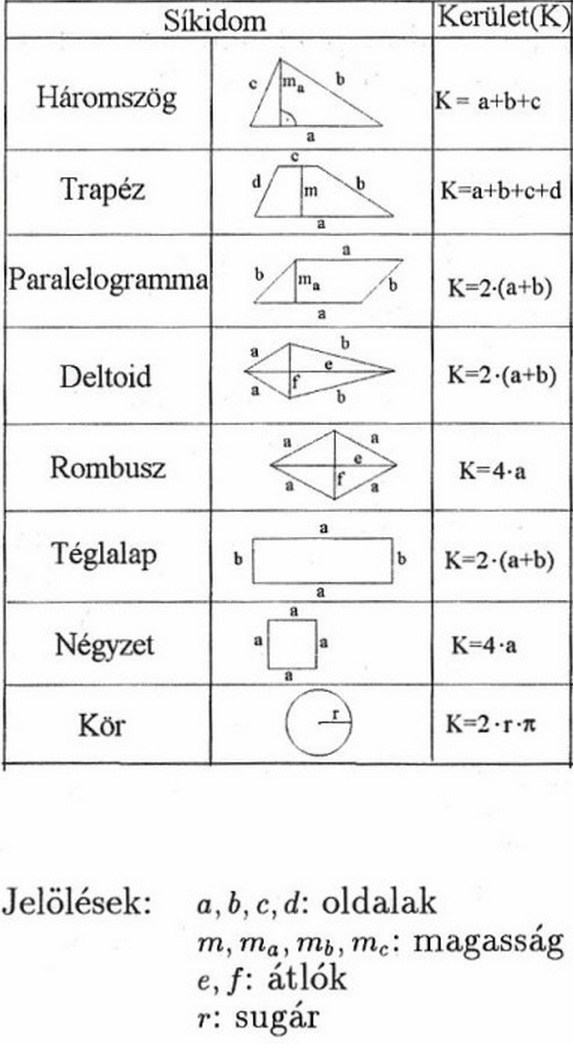
Folyóméter számítás a való életben:
Számoljuk ki egy szoba diletációs léc folyóméterét.
Legelső lépésként mérjük le a fal két oldalát, érdemes a fal mentén mérni, mivel oda kerül majd a léc is és a mérésünk is egyenes lesz, mivel ha srégen mérünk, akkor nagyobb lesz a szám amit mérünk.
Majd jegyezzük fel a mért adatokat, lehetőleg azonos mértékegységben mérjünk. Legjobb ha cm-ben mérünk és a mérés befejeztével átváltjuk méterbe 100cm az 1 méter. (osztjuk 100-al) Így könnyeben kapjuk meg a folyómétert (fm), és nem utána kell átváltani.
A két számot összeadjuk és aztán megszorozzuk 2-vel. ((hosszúság + szélesség) x 2 = kerület)
Kerület számítási példa:
Nézzünk egy konkrét példát:
Van egy 345 cm széles és 567 cm hosszú kiskertünk amit szeretnénk teljesen körbekeríteni.
Ennek a kerítésnek a drótszükségletét az alábbiak szerint határozzuk meg.
Először átváltjuk a mértékegységeket méterbe: (345cm=3,45m) (567cm =5,67m)
Aztán az így kapott számokat összeadjuk egymással és megszorozzuk kettővel (3,45+5,67) x2 = 18,24 m
Tehát ehhez a bekerítéses példához 18,24 m, folyóméter drótra lesz szükségünk.
Ha pedig még maradnál egy kicsit, akkor egy-két korábbi cikkünket tudom ajánlani:
1 fm hány méter? Így számolj egyszerűen folyóméterben a mindennapokban!
Köszönöm a figyelmet!
Ha tetszett a cikk, ne felejtsd el megosztani barátaiddal vagy hozzászólásban megírni a véleményedet.
És ha szeretnél még hasonló tanácsokat olvasni, akkor iratkozz fel a hírlevelünkre és Likeolj minket a Facebookon!
Köszönöm(köszönjük) a nagyon hasznos cikkeket. 23 éves létemre végre megértettem a dolgokat! 🙂
Hálásan köszönöm a szerzőnek!!!!
Örülök, hogy neked is segíthettem!
Mindig bajban vagyok ezekkel a számításokkal, de remélem hogy most már könnyebben fog menni… köszönöm