Hogyan számítsuk ki a háromszög magasságát? – Egyszerű útmutató
A háromszög magasságának kiszámítása az egyik legfontosabb alapfogalom a geometriában. A magasság segítségével tudjuk meghatározni a háromszög területét, valamint számos más fontos számítást végezhetünk vele.
Nézzük meg, hogyan számíthatjuk ki ezt lépésről lépésre, mindezt érthető módon, gyakorlati példákkal alátámasztva.
Mi is az a háromszög magassága?
Egyszerűen fogalmazva, a háromszög magassága az az egyenes szakasz, amely a háromszög egyik csúcsától a szemközti oldalhoz (vagy annak meghosszabbításához) húzódik úgy, hogy merőleges legyen arra az oldalra. Ezt az oldalt alapnak nevezzük.
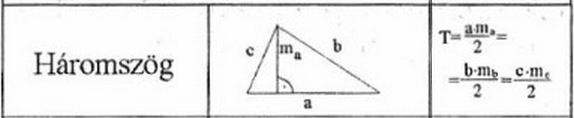
A háromszög magasságának képlete
Ha van egy háromszögünk, amelynek az alapja a, és a hozzá tartozó magassága m, akkor a háromszög területének képlete a következő:
T = (a * m) / 2
Innen kifejezhetjük a magasságot:
m = (2 * T) / a
Példa: Egy háromszög magasságának kiszámítása ismert területből
Tegyük fel, hogy van egy háromszög, amelynek területe 24 cm², és az alapja 8 cm. A magasság kiszámításához alkalmazzuk a fenti képletet:
m = (2 * 24) / 8
m = 48 / 8
m = 6 cm
Tehát a háromszög magassága 6 cm.

Gyakorlati példák a mindennapokban
1. Példa: Egy téglalap alakú háromszög
Ha egy téglalap átlója két háromszögre bontja a téglalapot, és a téglalap szélessége az alapunk, akkor a magasság megegyezik a téglalap magasságával. Tegyük fel, hogy a téglalap alapja 10 cm, a területe 50 cm². Ekkor:
m = (2 * 50) / 10
m = 100 / 10
m = 10 cm
2. Példa: Egyenlő oldalú háromszög
Egy 10 cm oldalhosszúságú egyenlő oldalú háromszög esetén a magasságot úgy számíthatjuk ki, hogy alkalmazzuk a speciális képletet:
m = (√3 / 2) * a
m = (√3 / 2) * 10
m ≈ 8.66 cm
A háromszög magassága más megközelítéssel
A magasságot kiszámíthatjuk trigonometriával is, ha ismerjük a szögeket. Például, ha van egy derékszögű háromszögünk, ahol az egyik szög α és az alap a, akkor a magasság:
m = a * tan(α)
Összefoglaló háromszög ma
A háromszög magasságának kiszámítása különböző módokon történhet, attól függően, hogy milyen információk állnak rendelkezésünkre. Gyakorlati alkalmazása nemcsak a geometriában, hanem a mindennapi életben is hasznos lehet, például építkezések vagy műszaki rajzok során.
Remélem, hogy ezek a példák segítenek abban, hogy magabiztosan számíthassátok ki bármely háromszög magasságát!

Hogyan számítsuk ki a paralelogramma magasságát?
A paralelogramma magassága szintén egy fontos geometriai fogalom, amely segít meghatározni a területét. A magasság itt is az alapra merőleges szakasz, amely a paralelogramma egyik oldalától a szemközti oldalhoz húzódik.

A paralelogramma területének képlete
A paralelogramma területét a következő képlettel számítjuk ki:
T = a * m
ahol a az alap hossza, m pedig a magasság. Innen a magasság kifejezhető:
m = T / a
Példa: A paralelogramma magasságának kiszámítása ismert területből
Tegyük fel, hogy egy paralelogramma területe 60 cm², és az alapja 12 cm. A magasság kiszámítása a fenti képlet alapján:
m = 60 / 12
m = 5 cm
Tehát a paralelogramma magassága 5 cm.
Gyakorlati példa a mindennapokban
1. Példa: Tetőszerkezet számítása
Ha van egy tetőszerkezetünk, amely paralelogrammára hasonlít, és tudjuk, hogy az alap hossza 15 m, a területe pedig 90 m², akkor a magasság:
m = 90 / 15
m = 6 m
Ez azt jelenti, hogy a tető magassága 6 m.
Összefoglaló paralelogramma ma
A paralelogramma magasságának kiszámítása is hasonló módszereket igényel mint a háromszögé, és mindkettő alapvető a geometriai feladatokban. Akár építészeti tervezésben, akár egyszerű rajzok készítésekor, ezek a képletek és megközelítések segíthetnek abban, hogy pontos számításokat végezzünk.

Összességében
A háromszög és a paralelogramma magasságának kiszámítása alapvető fontosságú a geometriában, de a mindennapi életben is számos gyakorlati alkalmazása van. Legyen szó építkezésről, tervezésről vagy egyszerű geometriai feladatokról, a megfelelő képletek és módszerek ismerete segít abban, hogy pontos és megbízható számításokat végezzünk.
Az ilyen számítások megértése és alkalmazása biztosítja, hogy magabiztosan kezelhessünk bármilyen kapcsolódó kihívást, legyen az egy egyszerű rajz vagy egy összetett építészeti projekt.
Ha pedig még maradnál kicsit, akkor egy-két korábbi cikkünket tudom ajánlani:
A négyzetméter számítás rejtelmei!
A Wiképidiáról kicsi érdekesség még…
Köszönöm a figyelmet!
Ha tetszett a cikk, ne felejtsd el megosztani barátaiddal vagy hozzászólásban megírni a véleményedet.
És ha szeretnél még hasonló tanácsokat olvasni, akkor iratkozz fel a hírlevelünkre és Likeolj minket a Facebookon!

Be the first to comment on "Izgalmas útmutató a háromszög és paralelogramma magasságának kiszámításához"