Ebben a cikkben egy olyan téma kerül terítékre, ami első hallásra talán túl szakmai vagy bonyolultnak tűnhet, de valójában nagyon is közel áll a mindennapjainkhoz.

Foglalkozni fogunk a henger űrtartalmának számításával, ami egy alapvető matematikai feladat, és rámutatok, hogy ez hogyan jelenik meg a hétköznapi életünkben.

Lássuk, hogyan lehet ezt a matematikai fogalmat egyszerűen és érthetően megközelíteni!

A henger alakú tárgyak mindenhol körülvesznek minket. Legyen szó egy italos dobozról, egy sima palackról vagy akár egy belsőégésű motorról, nagyon gyakran találkozunk ezzel a formával. De vajon tudjuk-e, hogy pontosan mennyi folyadékot, vagy egyéb anyagot képesek tárolni? Ez a tudás nemcsak kíváncsiságból fontos, hanem sok praktikus helyzetben is jól jöhet.

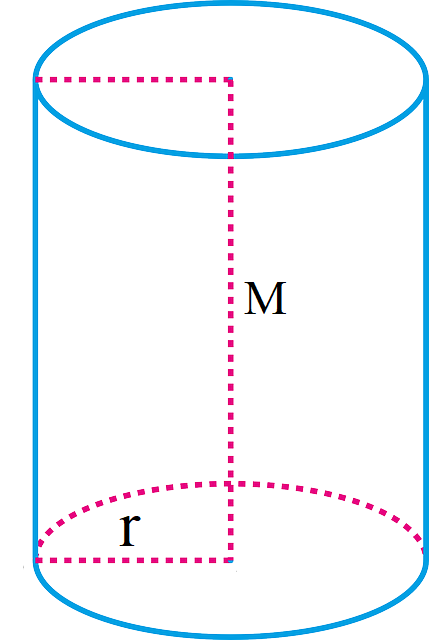
Először is tisztázzuk, mit is értünk henger alatt. Egy geometriai alakzat, amelynek két párhuzamos, egybevágó kör alakú alapja és oldallapja van.

A henger űrtartalmát a következő képlettel számoljuk ki: (V = r2* π * m), ahol (V) az űrtartalom, (r) a sugár, és (m) a magasság.

Képzeljünk el egy átlagos 0,33 literes italos dobozt. Hogyan számolhatjuk ki annak űrtartalmát? Először is mérjük meg az átmérőjét és a magasságát. Mondjuk az átmérő 6 cm, így a sugár 3 cm, a magassága pedig 12 cm. A képletbe behelyettesítve: (V=3,14*32*12=339 cm³). Ez azt jelenti, hogy a doboz körülbelül 0,339 liter folyadékot képes tárolni.

Nem csak elméletben érdekes a henger űrtartalmának számítása, hanem számos praktikus helyzetben is hasznosíthatjuk.

1. Háztartási tárolás:
Tegyük fel, hogy szeretnénk egy henger alakú edényt vásárolni liszt vagy cukor tárolására. Ha tudjuk a kívánt mennyiséget, a henger űrtartalmának számításával könnyen kiválaszthatjuk a megfelelő méretű tárolót.

2. Ipari használat:
Vegyünk például egy gyárat, ahol henger alakú tartályokban tárolnak folyadékokat. A tartály űrtartalmának ismerete segít a gyártási folyamatok optimalizálásában és a tárolási kapacitás hatékony kihasználásában.

3. Építészet és várostervezés:
Gondoljunk csak a víztoronyra, ami gyakran henger alakú. A tervezőknek tudniuk kell, mennyi vizet képes tárolni, hogy biztosíthassák a város vízellátását.

4. Kertészkedés:
Ha van egy henger alakú víztárolónk a kertben, a űrtartalom számítása segíthet meghatározni, mennyi vizet tudunk felhasználni a növényeink öntözéséhez.

5. Gépjármű ipar:
A járművek motorjainak a löktérfogatát, hengerűrtartalmát is így határozzák meg. Általában cm³, a nagyobb teljesítményű motoroknál literben adják meg.

A henger űrtartalmának számítása nem csak egy egyszerű matematikai művelet, hanem egyfajta kapcsolatot teremt a két- és háromdimenziós geometria között. A kör területének és a henger magasságának kombinációjával kapjuk meg az űrtartalmat, ami egy izgalmas matematikai és fizikai összefüggést tár fel előttünk.

A matematikai logika mögött a kör területének és a henger magasságának összeadása áll, ahol a π (pi) értéke a kör kerületének és átmérőjének összefüggését mutatja. Fizikailag pedig ez az űrtartalom kiszámítása segít meghatározni, hogy mennyi anyagot képes egy adott henger tárolni, legyen szó folyadékról, gázról vagy akár szilárd anyagról.

A henger űrtartalmának kiszámítása tehát nem csak egy matematikai kíváncsiság, hanem egy hasznos eszköz a mindennapi életünkben. Legyen szó otthoni tárolásról, ipari alkalmazásokról, építészetről vagy kertészkedésről, ez a tudás segíthet jobban megérteni és hatékonyabban kezelni a körülöttünk lévő világot.

1. Kozmetikai termékek:
Egy henger alakú szempillaspirál esetében az űrtartalom segíthet a fogyasztóknak megérteni, mennyi festéket kapnak valójában.

2. Szórófejes vízpermetező:
A henger alakú vízpermetező űrtartalmának ismerete segít a kertészeknek hatékonyabban tervezni a locsolást, permetezést.

3. Fényáteresztő hengerlencse:
Az optikai tervezők számára fontos lehet a lencsék űrtartalmának ismerete a pontos tervezés érdekében.

4. Építészetben a víztározó hengerek:
A víztározó hengerek, mint például a városi víztornyok, esetében az űrtartalom ismerete kulcsfontosságú a hatékony vízgazdálkodásban.

5. Motorok hengerűrtartalma:
A motorok tervezésekor és gyártásakor az egyik legfontosabb szempont a hengerűrtartalom meghatározása. Egy motor hengerűrtartalma alapvetően befolyásolja annak teljesítményét és üzemanyag-fogyasztását. Egy autómotor esetében a hengerűrtartalom azt mutatja meg, hogy a motor hengereiben mennyi levegő-üzemanyag keveréket képes befogadni és elégetni egy adott ciklus alatt. Minél nagyobb a hengerűrtartalom, általában annál erősebb a motor, de ez egyben több üzemanyag-fogyasztást is jelenthet.

Ezek a példák jól illusztrálják, hogy a hengerűrtartalom számítása milyen széleskörűen alkalmazható a gyakorlatban, különösen a gépjárműiparban, ahol a motorok teljesítménye és hatékonysága alapvető jelentőséggel bír. A hengerűrtartalom meghatározása segít a mérnököknek és tervezőknek abban, hogy hatékonyabb, erősebb és gazdaságosabb motorokat hozzanak létre.

Összességében a henger űrtartalmának számítása nemcsak egy matematikai alapelv, hanem egy gyakorlati eszköz is, amely segít nekünk a mindennapokban. Ezáltal jobban megérthetjük a körülöttünk lévő világot és hatékonyabban gazdálkodhatunk a rendelkezésre álló erőforrásainkkal. Remélem, ez a cikk segített megérteni a henger űrtartalmának fontosságát és alkalmazását a hétköznapi életünkben!

Itt van egy korábbi cikkünk a m³ azaz a köbméterszámítás rejtelmeiről.

A Wiképidiáról kicsi érdekesség még…

Köszönöm a figyelmet!

Ha tetszett a cikk, ne felejtsd el megosztani barátaiddal vagy hozzászólásban megírni a véleményedet.

És ha szeretnél még hasonló tanácsokat olvasni, akkor iratkozz fel a hírlevelünkre és Likeolj minket a Facebookon!